14500번: 테트로미노
폴리오미노란 크기가 1×1인 정사각형을 여러 개 이어서 붙인 도형이며, 다음과 같은 조건을 만족해야 한다. 정사각형은 서로 겹치면 안 된다. 도형은 모두 연결되어 있어야 한다. 정사각형의 변
www.acmicpc.net
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
static int n;
static int m;
static int[][] map;
static boolean[][] visited;
static int[] dx = {1,-1,0,0};
static int[] dy = {0,0,1,-1};
static int ans = 0;
public static void main(String[] args) throws Exception{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken()); // 행
m = Integer.parseInt(st.nextToken()); // 열
visited = new boolean[n][m];
map = new int[n][m];
for(int i=0; i<n; i++){
st = new StringTokenizer(br.readLine());
for(int j=0; j<m; j++){
map[i][j] = Integer.parseInt(st.nextToken());
}
}
for(int i=0; i<n; i++){
for(int j=0; j<m; j++){
visited[i][j] = true;
dfs(i, j, map[i][j], 1);
visited[i][j] = false;
func(i, j);
}
}
System.out.println(ans);
}
// ㅗ,ㅓ,ㅏ,ㅜ 제외한 다른 모양 탐색
private static void dfs(int a, int b, int sum, int cnt){
if(cnt>=4){
ans = Math.max(ans, sum);
return;
}
for(int i=0; i<4; i++){
int x = a + dx[i];
int y = b + dy[i];
if(x>=0&&x<n && y>=0&&y<m){
if(!visited[x][y]){
visited[x][y] = true;
dfs(x,y,sum+map[x][y],cnt+1);
visited[x][y] = false;
}
}
}
}
// ㅗ,ㅓ,ㅏ,ㅜ 탐색
private static void func(int x, int y){
if(x-1>=0 && x<n && y-1>=0 && y+1<m)
ans = Math.max(ans, map[x][y-1]+map[x][y]+map[x-1][y]+map[x][y+1]);
if(x>=0 && x+1<n && y-1>=0 && y+1<m)
ans = Math.max(ans, map[x][y-1]+map[x][y]+map[x+1][y]+map[x][y+1]);
if(x-1>=0 && x+1<n && y>=0 && y+1<m)
ans = Math.max(ans, map[x-1][y]+map[x][y]+map[x][y+1]+map[x+1][y]);
if(x-1>=0 && x+1<n && y-1>=0 && y<m)
ans = Math.max(ans, map[x-1][y]+map[x][y]+map[x][y-1]+map[x+1][y]);
}
}
처음 문제 읽고 막막했는데 밑에 주의할점만 고려한다면 생각보다 쉬운 문제였다.
주의할 점!
① DFS 로 풀어야 한다. BFS는 불가능!
- DFS : '현재' 를 기준으로 인접한 점 탐색
- BFS : '시작' 을 기준으로 인접한 점 탐색

DFS, BFS 를 수행했을 때 위와 같은 차이가 있다.
이 문제는 '현재' 위치에서 인접한 점을 탐색하여 최대값을 구해야 한다.
총 4개의 연결되어있는 블록에서 최대값을 구해야하기 때문에, DFS탐색에서 depth=4인 경우를 찾아야 한다.
② ㅗ ㅜ ㅓ ㅏ 의 경우는 DFS로 탐색이 불가능하다.
위의 그림과 같이 ㅗ ㅜ ㅓ ㅏ 의 경우는 DFS탐색이 아닌 따로 예외처리 해주어야 한다.
왜냐면, ㅗ ㅜ ㅓ ㅏ 는 왔던 길을 다시 되돌아가야하는데 이는 DFS에서 행해지지 않기 때문이다.
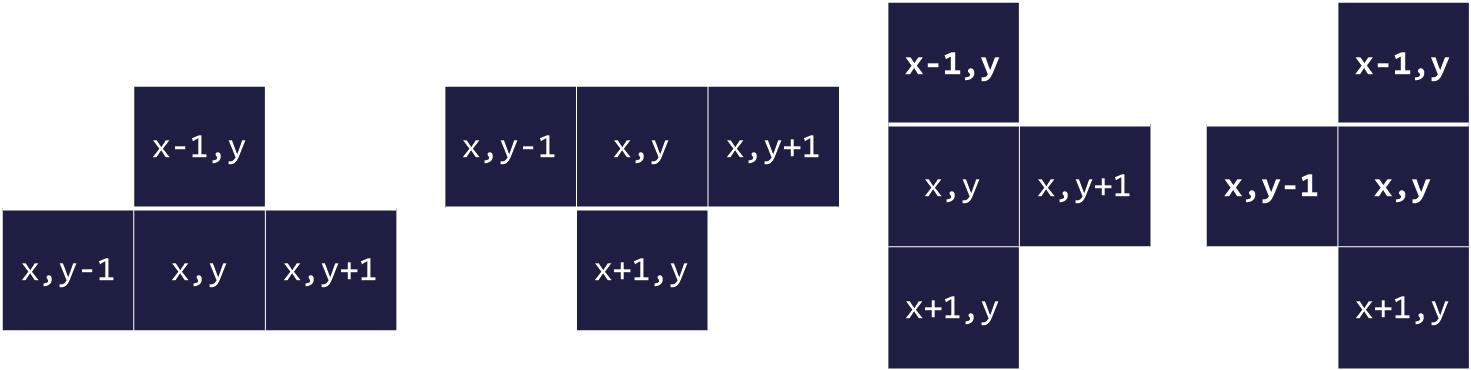
ㅗ ㅜ ㅓ ㅏ 는 제일 가운데를 (x행, y열) 로 표현했을 때 위의 그림과 같다.
이 네 가지 경우를 각각 구해서 ans값과 비교해 최대값으로 ans을 수정한다.
'1d-1c > BOJ' 카테고리의 다른 글
| 10972_다음 순열 & 10973_이전 순열 (JAVA) (0) | 2020.11.24 |
|---|---|
| 9095_1,2,3 더하기 (JAVA) (0) | 2020.11.24 |
| 6588_골드바흐의 추측 (JAVA) (0) | 2020.11.22 |
| 9613_GCD 합 (JAVA) (0) | 2020.11.22 |
| 1934_최소공배수 (JAVA) (0) | 2020.11.22 |